Least Squares Migration: 1 of 2 Articles
I discuss the important similarities and distinctions between RTM (Reverse Time Migration), LS-RTM (Least Squares RTM), and FWI (Full Waveform Inversion), and also relate their fundamental reliance upon back-projection to Deep Neural Network training used in many machine learning pursuits.
Least-Squares Migration (LSM) in Traditional Formulism
Recorded seismic data is band-limited (in temporal frequency and spatial frequency, i.e., wavenumber), subsurface seismic illumination is highly non-uniform because of imperfect acquisition geometry and impedance heterogeneities in the subsurface, and seismic migration is not the mathematical inverse of modeling (see also below). Collectively, the images of the subsurface produced by conventional seismic migration do not recover the true reflectivity and resolution for known fundamental reasons.
The two most common forms of Least-Squares Migration (LSM) are pursued in either the image domain or the data domain, and which have a diverse range of implementation in the industry and academia.
What is common to all styles of LSM is the ambition to compensate for variable subsurface illumination, and correspondingly improve amplitude balance across migrated reflectivity images.
Furthermore, if implemented optimally, the spatial resolution in reflectivity images (the resolution of event truncations, fault planes, localized clinoform features, etc.) should also improve due to the higher wavenumber content in the images. Note that all LSM implementations widely used today do not attempt to update the velocity model.
In a future article I will address an evolution of LSM and FWI that simultaneous updates both velocity and reflectivity, but for the time being I will focus on 'traditional' LSM.
Despite the aforementioned inability of conventional depth migration to correctly recover that reflectivity model, the redundancy of subsurface information captured by (typically) many thousands of overlapping shot gathers does mean that much of the desired reflectivity information is in fact available in the collective dataset; and can indeed be recovered with a more sophisticated approach to seismic migration. This is the ambition of LSM.
The ‘Least-Squares’ phrase in LSM refers to the mathematics behind the premise of LSM. The following few sentences address the traditional mathematical formulism and then I describe common implementations of LSM in practical terms.
For recorded seismic data, dobs ≈ dmod = Lm, where L is an operator that transforms the model, m, into the modeled data, dmod.
More commonly, it is said that L maps the seismic data from the model space to the data space.
In FWI the desired model is subsurface velocity, and in migration the desired model is subsurface reflectivity.
Conventional depth migration produces an approximation to the reflectivity, mmig = L*dobs, where L* is the adjoint (matrix transpose) of the modeling operator L.
As noted, migration is not the inverse of a modeling operation, however, the reflectivity model, mest, can be recovered by pursuing a classic inverse solution as follows:
mest = (L*L)-1L*dobs (1)
In the manner also pursued in FWI, the data-space implementation of LSM recovers the model, m, by iteratively minimizing the objective function
åi||dmod,i(m) – dobs,i|| + e||m – mref|| with appropriate regularization terms.
In other words, an initial reflectivity estimate (the traditional migration image) is iteratively updated until the reflectivity is much closer to the truth than is recovered using traditional imaging.
I will now briefly explain how the historically more common implementation of equation (1) is pursued in the image domain by estimating L*L, and then I will explain the more correct data domain implementation of LSM.
The strong similarities to Reverse Time Migration (RTM), FWI and Deep Neural Network (DNN) training will become evident.
Image Domain LSM in Practical Terms
Image domain LSM explicitly computes L*L º H, where H is the Hessian matrix containing the desired subsurface illumination information. As the Hessian matrix is normally massive in size for modern 3D datasets, and too computationally intensive to compute directly, H is explicitly computed using a synthetic modeling-migration exercise (see below), but can also be approximated by moving-window matching filters applied to migrated data.
As shown in the figure below, Point Spread Functions (PSFs) representing the spatially-variable migration impulse response are computed by embedding a grid of point diffractors into the velocity model used for imaging, forward modeling each diffraction response, and then migrating the result.
Equation (1) then becomes mest = H-1mmig, remembering that mmig = L*dobs.
The implementation of this form of image domain LSM is therefore achieved by multi-dimensional deconvolution of the PSFs from the migration of the real data (hence the ‘image domain’ terminology). When done correctly, LSM yields a reflectivity image with higher wavenumber content (immediately below) and more uniform illumination (the synthetic modelling below).
(left) PSFs computed below a salt overhang in the Sigsbee2A synthetic model; (center) FK spectrum from traditionally-migrated data; and (right) FK spectrum after LSM, containing higher wavenumber amplitudes.
The PSFs can also be computed in an angle-dependent manner, thereby enabling pre-stack implementation. The imaging platform may be any solution such as Kirchhoff migration, one-way wavefield extrapolation migration, or two-way wavefield propagation migration (i.e., RTM). In practice, the choice of imaging platform is generally dictated by the complexity of the subsurface geology and the computational budget.
By comparison to traditional migration (upper), which often fails to recover the true earth reflectivity in areas affected by subsurface illumination variations and imperfect acquisition geometry, LSM (middle) recovers the reflectivity much closer to the true model (lower). If implemented correctly, local image focusing should be much sharper (e.g. the point diffractors embedded into the synthetic data model), and spatial resolution should be better due to the improvement in high wavenumber content (e.g. local event terminations and fault plane imaging).
Note that all implementations LSM today do not update the velocity model used for imaging.
Data Domain LSM in Practical Terms
Alternatively, an implicit LSM approach in the data domain solves equation (1) and recovers the operator L via a linearized optimization approach. In practice, this involves the iterative updating of the desired reflectivity model in a manner analogous to the iterative updating of the desired velocity model via non-linear inversion in FWI.
As shown schematically in the following figure, data domain LSM is pursued as follows:
- Each recorded shot gather is initially migrated in the traditional manner, for example, using RTM: A source wavelet is injected into the velocity model at each shot location, and forward-propagated (modeled) source wavefield snapshots are stored memory for each appropriate depth step.
- Each recorded shot gather is injected into the model at all receiver locations, starting with the largest recorded time sample. The ‘back-propagated receiver wavefield’ is also stored as a series of wavefield snapshots.
- An imaging condition recovers an image from appropriate pairs of source and receiver wavefields wherever the two wavefields are kinematically equivalent at the various subsurface locations, this process is repeated for all source and receiver wavefield snapshots, and the results are summed to produce the ‘partial’ image for each shot gather, and these partial images are summed to yield the reflectivity model, m.
- The reflectivity model, m, is then used to model each shot gather using Born modeling (dsyn), and the residual reflectivity for each shot gather is computed from (dobs – dsyn).
- This residual shot gather is then used when back-propagating the receiver wavefield in RTM. The forward-propagation step is identical to the initial migration. The reflectivity from this residual migration step is added to the model, m.
- Iteration continues until the norm of the (regularized) objective function becomes acceptably small.
- It follows that the shot gather modeled in the final iteration is a match to the recorded shot gather at each location, but the reflectivity model, m, will be much closer to the truth than was initially recovered using traditional RTM.
Schematic workflow for data domain (iterative) LSM. Each iteration involves one (Born) modeling step and one migration, and a residual shot gather is migrated and used to update the reflectivity model.
Note that data domain LSM can also compute highly accurate angle domain common image gathers (ADCIGs) for various forms of pre-stack analyses.
RTM, Data Domain LSM, and FWI
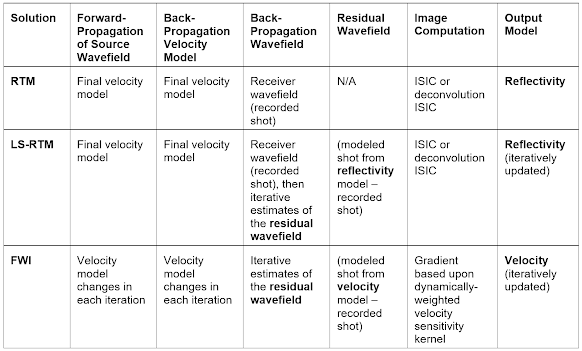
The following table compares the main elements of RTM, (data domain) LS-RTM, and FWI.
*ISIC = Inverse Scattering Imaging Condition
Comparison between the components of RTM, data domain LS-RTM, and FWI.
Whereas RTM and LS-RTM assume the velocity model is final, FWI updates the model during each iteration. The forward-propagated source wavefield and the back-propagated residual wavefield therefore both use different velocity models during each FWI iteration.
LS-RTM back-propagates the residual reflectivity information during each RTM-based update of the reflectivity model. In a more complex workflow, FWI back-propagates the residual reflectivity information and then computes the gradient as an RTM image that is then converted to a velocity model update.
Note that PGS use an imaging condition within RTM known as the ‘Inverse Scattering Imaging Condition’ (ISIC). Traditional RTM correlation methods can be negatively affected by backscattered and turning waves in the modeling process, which causes the incident and reflected wavefields to be in phase at locations that are not the reflection points. This results in strongly correlated noise in the seismic image.
The ISIC has been designed to reduce the imaging noise by using directional information computed directly from the data. ISIC is based on a generalized inverse scattering imaging condition in which the backscattered waves are attenuated by using the combination of two separate images: one based on the product of the time derivatives of the incident and reflected wavefields, and the other based on the product of the spatial gradients of the incident and reflected wavefields. These images are then combined to produce the final inverse scattering image.
A Deconvolution ISIC has also been developed that improves the resolution of both pre-stack and post-stack RTM reflectivity, and that produces amplitudes that are more directly related to the true reflection coefficient.
The ‘true’ earth model (left) can be regarded as the sum of the background model recovered by FWI (low wavenumbers: center) and the reflectivity recovered during imaging (high wavenumbers: right).The ‘true’ earth model can be regarded as the sum of the background model recovered by FWI (low wavenumbers) and the reflectivity recovered during imaging (high wavenumbers). As illustrated here, LSM will recover a more complete model of the reflectivity.
Linking Pre-Stack and Post-Stack Illumination
The following figure uses a North Sea example of high-velocity injectite features in the overburden.
Full wavefield FWI using diving waves, refractions and reflections has recovered an excellent high-resolution velocity model over all depths of exploration from 8km multisensor GeoStreamer data (upper left panel). The high-velocity anomalies spatially coincident with the injectite features are clearly associated with illumination variations in the deeper subsurface (upper right panel).
Illumination overlays such as this are produced by extracting the main diagonal information in the Hessian matrix computed during image domain LSM. The lower panel in shows illumination as an offset-dependent color overlay on NMO-corrected offset domain common image gathers (ODCIGs).
In this example, the ODCIGs were produced with Kirchhoff image domain LSM. Overall, these examples illustrate the considerable flexibility available when a portfolio of image domain and data domain LSM solutions are available for both pre-stack and post-stack application.
Note that the illumination compensation applied by LSM applies to both source and receiver side effects, whereas the ‘illumination compensation’ applied within some conventional imaging solutions only affects the source considerations.
In some scenarios, the application of LSM prior to amplitude-based studies may be beneficial to the recovery of the amplitude vs. angle (AVA) gradient without contamination by illumination effects.
Coherence attribute depth slices computed from data domain LSM imaging in the Orphan Basin, offshore Eastern Canada; (lower) Coherency depth slices overlain with the FWI depth velocity model in colour. Note the excellent spatial resolution and correlation of the FWI velocity model at all depths with the reflectivity features derived from LSM! The full wavefield FWI solution has recovered excellent resolution to at least 5.2km using 8.1km multisensor streamer lengths, and data domain LSM has correspondingly recovered excellent high wavenumber spatial resolution over all depths of exploration interest. Courtesy of PGS, TGS, and OilCo NL.
The figure above presents a series of high-resolution FWI and data domain LSM depth slices from the Orphan Basin in offshore Eastern Canada. A coherency-based attribute was applied to the LSM volume to enhance local high-frequency features.
The upper panel shows depth slices between 2.7 km and 5.2 km, highlighting the power of LSM to enhance reflectivity and spatial resolution over a large range of depths.
The lower panel overlays the full wavefield FWI velocity model in color. A remarkable spatial correlation between high-resolution velocity model features and the LSM coherency attributes is observed; even to 5.2 km depth using a conventional 8.1 km multisensor GeoStreamer spread.
Back-Propagation of Deep Neural Network Training Errors
The back-propagation principles discussed here are shared with the training of Deep Neural Networks (DNNs) commonly used for an increasingly diverse range of machine learning applications in our industry.
Schematic representation of a Deep Neural Network (DNN). In this arbitrary example with three (dense) hidden layers, eight input samples yield four output values.
The figure above shows a schematic DNN used to four output values from eight input values. In this simple cartoon, the third hidden layer is a ‘dense’ layer wherein each neuron is connected to every neuron in the second hidden layer. In compact vectorized (matrix) form, the activation of each layer, l, can be written as follows:
al = s(wlal-1 + bl) (2)
Where wl is the weight vector from layer l-1 to layer l, al is the activation vector for layer l, al-1 is the activation vector for layer l-1 (i.e. the output from the previous layer; which could be the input x in the case of the first hidden layer), bl is the bias vector (effectively threshold values to influence the nature of activation in the next layer) for layer l, and s is some function.
In the schematic example above, the activation (a) of one particular neuron in the third layer is highlighted in terms of one particular neuron in the second layer. In practice, the weight is uniquely defined for each neural pathway.
The term inside the parenthesis in equation (2) above is a linear operation, however, the function s may often be a non-linear operation; such as sigmoid functions (compress weights to be in the range of 0-1), hyperbolic tangent (compress weights to be in the range of ±1), rectified linear unit (ReLU) operations (preserve only the positive values), and so on.
With appropriate design, the DNN can be applied to apparently limitless Artificial intelligence (AI) pursuits well beyond the scope of this discussion, but emerging applications in the seismic exploration workflow include automated seismic interpretation (event picking, fault plane interpretation, geobody extraction, etc.), automated QC in seismic acquisition and processing, preconditioning of the input data to FWI to avoid cycle-skipping, and so on.
In simple terms, DNNs are ‘trained’ by back-propagating a cost function in some kind of gradient descent exercise. The cost function is computed by comparing the output values from training data to their known (labeled) values.
In practice, the data from a study are separated into ‘training’ data with labeled values and the unlabeled data that the trained network is applied to.
To accommodate the large size of typical training datasets, the training data are commonly split into randomly-selected mini-batches.
In the first ‘epoch’ of network training with all the batches, each neuron’s values of w and b are set to random values, and the first mini-batch of training data is forward-propagated through the network to produce a vector of output values.
A cost function is computed, used within a stochastic gradient descent process to back-propagate the cost, and the updates to each (unknown) network parameter is driven by how much the change in each parameter value contributed to the change in the cost function.
This process is repeated for all the batches, and once all the batches have been used, that epoch is complete, and the process starts again with a re-shuffling of the full training dataset; generally until the cost function indicates that the global minima in network weight and bias values has been computed.
As with the scenarios for FWI and LSM, much DNN R&D is being invested in the determination of optimum initial weights, and the pursuit of regularization to prevent over-fitting (which may in practice simply be network architectures that pursue model generalization, rather than classic regularization).
Summary
I discussed the workflow strategies for both image domain and data domain Least-Squares Migration (LSM) in both classical and practical terms. When applied correctly, LSM can use many common seismic imaging platforms, and can be applicable to both pre-stack and post-stack seismic data. An improved estimate of the reflectivity model should also demonstrate better spatial resolution (associated with higher wavenumber content).
Image domain LSM explicitly computes a form of the Hessian matrix, which is used to ‘de-blur’ a migrated image via a multi-dimensional deconvolution of the Hessian.
Data domain LSM pursues an iterative minimization of an objective function based on the difference between the observed data and synthetic data modeled from the reflectivity at each iteration.
I then compared the similarities between RTM, data domain LS-RTM and FWI, in terms of the iterative back-propagation of either receiver wavefields (RTM) or residual wavefields (LS-RTM and FWI) used as boundary conditions to the model.
The specific terminology used by technical practitioners is that each method uses the ‘Adjoint Source’ during propagation, but I avoided this terminology in the text. For RTM there is no iterative updates to either the velocity of reflectivity model. For data domain LS-RTM the reflectivity model is updated, and for FWI the velocity model is updated. It is noted that although the gradient computed within each FWI iteration is an RTM image of reflectivity, this is converted to an update to the velocity model.
FWI and RTM / LS-RTM (or indeed, any imaging method) can also be related in terms of their complementary wavenumber contributions to our estimate of the ‘true’ earth model: FWI recovers the low wavenumber background model, and imaging recovers the high wavenumber reflectivity.
Although not explored here, it follows that the industry vision of recovering true earth models from field measurements (shot gathers) must integrate the mathematics central to both FWI and LSM.
Finally, I noted that Deep Neural Network (DNN) training also pursues a back-propagation of errors computed within a cost function; analogous in some ways to the back-propagation methods used for FWI, RTM and data domain LSM.
Acknowledgements
I am particularly indebted for countless technical discussions with Nizar Chemingui (PGS), Cyrille Reiser (PGS), and Øystein Korsmo (PGS).
.
Interested in Hearing More?
- Least Squares Migration: 15-minute TechByte webinar.
- Illumination vs AVO: 11-minute TechByte webinar.
Disclaimer
The content discussed here represents the opinion of Andrew Long only and may not be indicative of the opinions of Petroleum Geophysical AS or its affiliates ("PGS") or any other entity. Furthermore, material presented here is subject to copyright by Andrew Long, PGS, or other owners (with permission), and no content shall be used anywhere else without explicit permission. The content of this website is for general information purposes only and should not be used for making any business, technical or other decisions.










Comments
Post a Comment